ニワトリはなぜ道を渡らなかったのか
その答えは
ニワトリは道を渡れるはずがないから
である
???
一体何を言っているのでしょう?
このことを真面目に考えた人が古代ギリシアの哲学者ゼノンでした
今回はこのゼノンとゼノンの哲学の一部を紹介します
ゼノンとはどんな人
ゼノンは今の南イタリアにあったギリシアの植民都市エレアに住む哲学者でした
ゼノンはエレア派の創始者パルメニデスに養子縁組され、生涯の弟子、そして愛人となったとされます
パルメニデスのエレア派は、アルケー(万物の根源)を観察しており、「有/無」という概念を提唱したと言われています
他のアルケーを唱えた人たち
ゼノンもエレア派の哲学者として「ニワトリはなぜ道を渡らなかったのか?」に代表される「ゼノンのパラドックス」を唱えました
ゼノンは、エレアの僭主を打倒しようとし、捉えられ殺害されてしまいます
ゼノンは僭主の耳に噛みつき、耳を噛みちぎった後に処刑されました
ゼノンのパラドックスとは?
ゼノンは多くのパラドックスを唱えています
パラドックスとは日本語では逆説とされています
常理に反する説で、その説に反発する正当な論拠を見いだしがたいもの。歴史的には「アキレウスは亀に追いつけない」などのゼノンの逆説が名高い。逆理。パラドックス。
コトバンクより抜粋引用
ゼノンの唱えた主なパラドックスは次のようなものです
- 多のパラドックス
- 運動のパラドックス
- 二分法
- アキレスと亀
- 飛んでる矢は止まっている など
この中から二分法とアキレスと亀について紹介します
二分法とは
二分法とは最初の「ニワトリはなぜ道を渡らなかったのか?」「渡れるはずがないからだ」を説明したもので、以下のように説明されています
- ニワトリは目的地へ向かうために出発します
- 半分まで到達した時に、残りが半分であることに気づきます
- 全体の4分の3まで到達した時に、中間地点から半分進んだことと残りが半分の半分になったと気づきます
- さらに半分進んだ時に、残りが半分あることに気づきます
- そして永遠に半分残ると言ったことが起き、永遠にゴールには着かないことに気づきます
と言ったものです
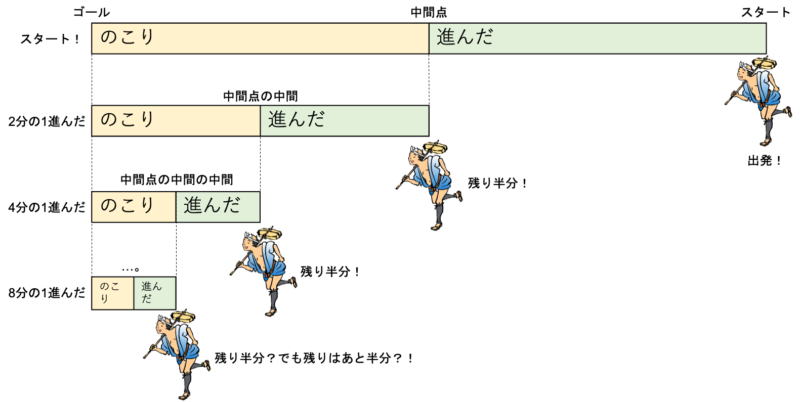
言葉にするとわかりずらいので図を書きました
ゴールには近づくのですが、常に残りがあり決して残りが0になることはないというのが二分法の言いたかったことだと思います
実際は皆ゴールしちゃうので違うと感じるかもしれませんが、考えるとうなづけますよね
これがパラドックスです
アキレスと亀
うさぎとカメの童話を知らない人は少ないと思います
ここでは、真面目に頑張った方が最後は勝つよという話ではなく
うさぎとカメの進むスピードの違いを例に取っています
うさぎとカメではうさぎの方が早いために、カメにハンデを与えて、後からうさぎが出発します
果たしてうさぎは亀に追いつけるのでしょうか?という話です
我々の経験からすれば「追いつける」というのが真理ですが
ゼノンは「追いつけない」ということを説明しています
理由はこうです
- うさぎが出発する時、亀はうさぎの前を進んでいます
- うさぎが亀がいた地点まで到着した時、亀はさらに前を進んでいます
- うさぎがさらに亀がいた地点に到着した時、亀はもっと前を進んでいます
- うさぎが追いつけば亀は常に前にいることになるので永遠に追いつけない
こう言った説明です
これも図解してみました

この説明には現在私たちが習う数学において、速度の概念が欠落しているので実際は追いつくのですが、目的が動いているうちは追いかけても追いつけないということを言っていました
ゼノンのパラドックスが残したもの
これらのパラドックスは、のちの哲学者たちに反証の機会を多く与えました
これらの反証から現在の数学や物理の発展に大きく影響を与えたと言われています
二分法やアキレスと亀が今の生活において成り立たないのは実体験からわかりますが、なぜそうなるのかということ考える機会を与えたのがゼノンだと言えます
このほかにもゼノンは面白いパラドックスを唱えていますので、興味が出た人は調べてみるといいと思います
哲学的な内容の話なので、ゆっくりと読んだ方が理解しやすいと思います
(アルケー)万物の根源についてはこちらも参照してみてください